Migrating text metrics to pure Haskell
haskellPublished on June 13, 2017
It’s been a while since I first published the text-metrics package,
which allows to calculate various string metrics using Text values as
inputs. Originally the package was written primarily in C with wrappers in
Haskell. At the time I needed maximal speed and did not care whether the
algorithms themselves are coded is C or Haskell, as long as they work, and
work fast.
However, recently there were quite inspiring blog posts about Haskell
competing with C in terms of speed and memory consumption. One such a blog
post is Chris Done’s “Fast Haskell: Competing with C at parsing XML”,
which is a most entertaining read. Now that I have more free time I decided
to go back to text-metrics and rewrite it in pure Haskell. The benefits
are:
-
Things like GHCJS will be able to use the package.
-
Pure Haskell is hopefully more cross-platform. Can’t really tell whether there are any issues with compiling packages with C bits on Windows nowadays, because I have not had access to a Windows machine for 3 years.
-
The C implementation does not work correctly when the inputs contain characters from a tiny subset of Unicode that is represented by more than one
Word16value per character. This subset includes historic scripts, emoji, and less-used Chinese ideographs. It would be good to make the functions work correctly with those characters as well. -
One more proof that Haskell can be quite fast when it is necessary.
Hamming distance
I decided to start with the simplest algorithm in text-metrics: hamming
distance. This distance is only defined for inputs of equal length, so the
signature looks like this:
hamming :: Text -> Text -> Maybe Natural
Well, at least it did. I decided to replace Natural with Int, because
all the functions we are going to use take and return Ints, so it’s no use
trying to push proper types like Natural (which is also slower to work
with).
Hamming distance is just the number of characters at the same indices that are different. So the C implementation was:
unsigned int tmetrics_hamming (unsigned int len, uint16_t *a, uint16_t *b)
{
unsigned int acc = 0, i;
for (i = 0; i < len; i++)
{
if (*(a + i) != *(b + i)) acc++;
}
return acc;
}
Looks dead-simple, but how to do the same in Haskell efficiently? Well,
first of all we need an efficient way to traverse Text values character by
character. We should remember that Text is a lot like a list of Word16
values internally. As I mentioned, some characters are represented as two
consecutive Word16 values, and most characters are just one Word16. So
we don’t know which is which, and that essentially makes it impossible to
have
indexing
in O(1).
So we can’t access a character at a certain offset (as in *(a + i)), we
should perform something like synchronous unconsing on both Text values
(good that they are of the same length!). The text package provides tools
for this in
Data.Text.Unsafe.
The Iter data type is our friend:
data Iter = Iter {-# UNPACK #-} !Char {-# UNPACK #-} !Int
The Char value is an “unconsed” character and Int is the length of the
character as a number of Word16 values (1 or 2). We will use three
functions:
-
iter :: Text -> Int -> Iter—O(1) iterate (unsafely) one step forwards through a UTF-16 array, returning the current character and the delta to add to give the next offset to iterate at. -
iter_ :: Text -> Int -> Int—O(1) iterate one step through a UTF-16 array, returning the delta to add to give the next offset to iterate at. -
lengthWord16—O(1) return the length of aTextin units ofWord16.
That said, here is a Haskell implementation of Hamming distance:
hamming :: Text -> Text -> Maybe Int
hamming a b =
if T.length a == T.length b
then Just (go 0 0 0)
else Nothing
where
go !na !nb !r =
let !(TU.Iter cha da) = TU.iter a na
!(TU.Iter chb db) = TU.iter b nb
in if | na == len -> r
| cha /= chb -> go (na + da) (nb + db) (r + 1)
| otherwise -> go (na + da) (nb + db) r
len = TU.lengthWord16 a
First we have to confirm that the input values are of the same length. Due
to the reasons mentioned earlier, we have to traverse each of them to
compute their lengths. If the lengths are equal we can start counting
characters that are located at the same positions but are different. go is
a tail-recursive helper that steps through the Text values using iter.
na and nb are the indices we use to iterate over internal arrays of
Word16 values, we increment them by da and db respectively. The result
is accumulated in r. The strictness annotations in the form of bang
patterns were optional in this case as GHC was able to figure out strictness
itself, but I decided to keep them there, just in case.
Let’s see if we are close to the C implementation with this:
| Case | Allocated | Max |
|---|---|---|
| hamming (C)/5 | 1,360 | 400 |
| hamming (C)/10 | 2,408 | 688 |
| hamming (C)/20 | 4,056 | 1,096 |
| hamming (C)/40 | 6,056 | 1,368 |
| hamming (C)/80 | 8,504 | 1,464 |
| hamming (C)/160 | 13,384 | 1,656 |
| hamming (Haskell)/5 | 1,344 | 400 |
| hamming (Haskell)/10 | 2,392 | 688 |
| hamming (Haskell)/20 | 4,040 | 1,096 |
| hamming (Haskell)/40 | 6,040 | 1,368 |
| hamming (Haskell)/80 | 8,488 | 1,464 |
| hamming (Haskell)/160 | 13,368 | 1,656 |
The weigh report shows that memory consumption is essentially the same. And here is a Criterion benchmark:
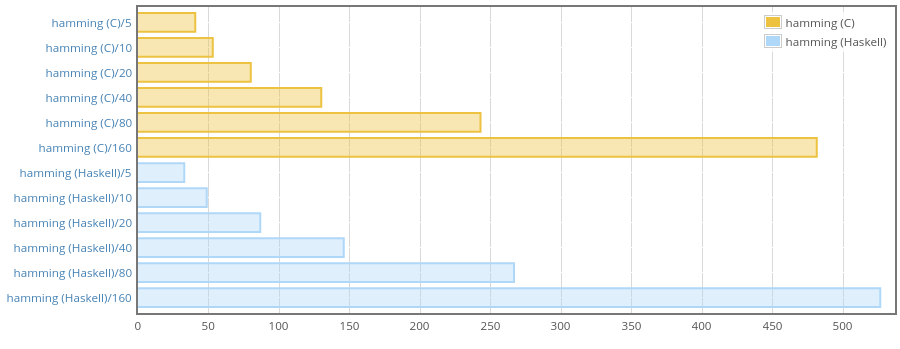
This shows that the new pure Haskell implementation is not slower. In fact,
it’s even a bit faster for short strings. The result can be explained by the
fact that to pass Text to C it has to be copied, with pure Haskell
implementation we avoid the copying.
Jaro distance
The Jaro distance \(d_\text{j}\) of two given strings \(s_\text{1}\) and \(s_\text{2}\) is
\[d_\text{j} = \begin{cases} 0 & \quad \text{if } m = 0 \\ \frac{1}{3} \left(\frac{m}{|s_\text{1}|} + \frac{m}{|s_\text{2}|} + \frac{m-t}{m}\right) & \quad \text{otherwise} \\ \end{cases}\]
Where
- \(|s_\text{i}|\) means the length of the string \(s_\text{i}\);
- \(m\) is the number of matching characters;
- \(t\) is half the number of transpositions.
Two characters from \(s_\text{1}\) and \(s_\text{2}\) respectively are considered matching only if they are the same and not farther than \(\left\lfloor\frac{max(|s_\text{1}|,|s_\text{2}|)}{2}\right\rfloor - 1\).
A matching pair is counted as a transposition also if the characters are close enough but in the opposite order. See more about this in the Wikipedia article.
The implementation is considerably more verbose for this one:
jaro :: Text -> Text -> Ratio Int
jaro a b =
if T.null a || T.null b -- (1)
then 0 % 1
else runST $ do -- (2)
let lena = T.length a
lenb = T.length b
d =
if lena >= 2 && lenb >= 2
then max lena lenb `quot` 2 - 1
else 0
v <- VUM.replicate lenb (0 :: Int) -- (3)
r <- VUM.replicate 3 (0 :: Int) -- tj, m, t (4)
let goi !i !na !fromb = do -- (5)
let !(TU.Iter ai da) = TU.iter a na -- (6)
(from, fromb') =
if i >= d
then (i - d, fromb + TU.iter_ b fromb)
else (0, 0)
to = min (i + d + 1) lenb
goj !j !nb =
when (j < to) $ do
let !(TU.Iter bj db) = TU.iter b nb
used <- (== 1) <$> VUM.unsafeRead v j
if not used && ai == bj
then do
tj <- VUM.unsafeRead r 0
if j < tj
then VUM.unsafeModify r (+ 1) 2
else VUM.unsafeWrite r 0 j
VUM.unsafeWrite v j 1
VUM.unsafeModify r (+ 1) 1
else goj (j + 1) (nb + db)
when (i < lena) $ do
goj from fromb
goi (i + 1) (na + da) fromb'
goi 0 0 0
m <- VUM.unsafeRead r 1
t <- VUM.unsafeRead r 2
return $
if m == 0
then 0 % 1
else ((m % lena) +
(m % lenb) +
((m - t) % m)) / 3
Inability to lookup characters at given index in O(1) was especially painful with this algorithm.
Some observations:
-
The
nullfunction is O(1) just like with linked list, we use it to detect the corner case when an input is the empty string. In that case we return zero, as it’s not clear how to apply the algorithm. -
The algorithm requires keeping track of a lot more things, not just indices in the internal arrays of
Word16values. So we need to use mutable unboxed vectors here. For that we need theSTmonad which we enter here. -
The
vvector is conceptually a vector ofBoolvalues, but using primitiveIntvalues here instead ofBools gives some speed up, especially with longer input values. I’m not entirely sure why this is so. Looking at the code ofData.Vector.Unboxed.Base, unboxedBoolis represented asWord8values (which makes sense becauseWord8has a primitive type inside, whileBoolis just a normal sum type). Maybe the conversion to and fromWord8takes some time? -
The
rvector holds all other auxiliary variables that we want to mutate. The thing here is that normal mutable references created withSTRefare not particularly fast, so we have to cheat like this. The variables that are stored inrare not modified very intensively, but still keeping them in an unboxed mutable vector gives a little speedup. The pattern is abstracted in themutable-contanterspackage which allows you to work with mutable unboxed vector of length 1 as with a special sort of efficient mutable variable.mutable-containersdepends onmono-traversablethough, which is completely unnecessary fortext-metrics, so I’ve chosen to work with bare mutable vectors here, which is ugly, but still not that hard. -
In this case GHC was not able to figure out strictness, so these bang patterns actually make a lot of difference (especially visible for longer inputs, where the algorithm is about ×10 slower without the strictness annotations).
-
Strictness annotations on pattern-matching on
Iterhelp quite a bit. Even though the innerCharandIntinIterare unboxed, theIteritself is a box, so forcing it proved to be a good thing.
| Case | Allocated | Max |
|---|---|---|
| jaro (C)/5 | 4,592 | 400 |
| jaro (C)/10 | 5,640 | 688 |
| jaro (C)/20 | 7,288 | 1,096 |
| jaro (C)/40 | 9,288 | 1,368 |
| jaro (C)/80 | 11,736 | 1,464 |
| jaro (C)/160 | 16,616 | 1,656 |
| jaro (Haskell)/5 | 5,680 | 400 |
| jaro (Haskell)/10 | 7,480 | 688 |
| jaro (Haskell)/20 | 10,696 | 1,096 |
| jaro (Haskell)/40 | 15,832 | 1,368 |
| jaro (Haskell)/80 | 24,560 | 1,464 |
| jaro (Haskell)/160 | 42,000 | 1,656 |
Memory consumption looks OK. Our Haskell implementation allocates more but
residency is the same as with C version (you can track max residency with
weigh-0.0.4 and later, I requested this feature some time ago and Chris
Done was kind enough to add it).
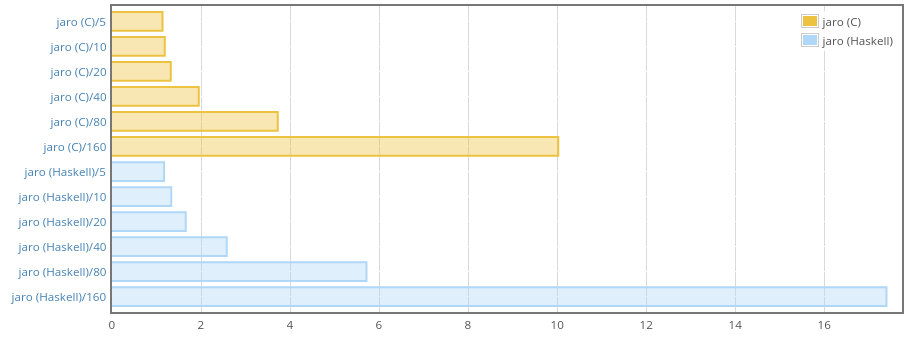
We are slower than C here, but for short strings there is almost no
difference, so I guess it’s OK as the package is mainly about working with
relatively short inputs. Do not forget that we’re also more correct with
this Haskell implementation because we iterate properly, taking into account
existence of characters that may take two Word16 cells in Text‘s
internal array.
There is also a function for Jaro-Winkler distance but it’s mostly the same, so let’s skip it.
Levenshtein distance
Finally, probably the most popular function is levenshtein, which
calculates the Levenshtein distance. The C implementation looks like
this:
unsigned int tmetrics_levenshtein
(unsigned int la, uint16_t *a, unsigned int lb, uint16_t *b)
{
if (la == 0) return lb;
if (lb == 0) return la;
unsigned int v_len = lb + 1, *v0, *v1, i, j;
if (v_len > VLEN_MAX)
{
v0 = malloc(sizeof(unsigned int) * v_len);
v1 = malloc(sizeof(unsigned int) * v_len);
}
else
{
v0 = alloca(sizeof(unsigned int) * v_len);
v1 = alloca(sizeof(unsigned int) * v_len);
}
for (i = 0; i < v_len; i++)
v0[i] = i;
for (i = 0; i < la; i++)
{
v1[0] = i + 1;
for (j = 0; j < lb; j++)
{
unsigned int cost = *(a + i) == *(b + j) ? 0 : 1;
unsigned int x = *(v1 + j) + 1;
unsigned int y = *(v0 + j + 1) + 1;
unsigned int z = *(v0 + j) + cost;
*(v1 + j + 1) = MIN(x, MIN(y, z));
}
unsigned int *ptr = v0;
v0 = v1;
v1 = ptr;
}
unsigned int result = *(v0 + lb);
if (v_len > VLEN_MAX)
{
free(v0);
free(v1);
}
return result;
}
Some buzz here is about choosing between malloc and alloca. alloca
allocates on the stack, while malloc allocates on the heap, so the latter
is slower. This is not particularly important though. What I like about this
implementation is that we can swap v0 and v1 by just swapping their
pointers, how to translate that into Haskell?
I’ve come up with this solution:
levenshtein :: Text -> Text -> Int
levenshtein a b
| T.null a = lenb
| T.null b = lena
| otherwise = runST $ do
let v_len = lenb + 1
v <- VUM.unsafeNew (v_len * 2)
let gov !i =
when (i < v_len) $ do
VUM.unsafeWrite v i i
gov (i + 1)
goi !i !na !v0 !v1 = do
let !(TU.Iter ai da) = TU.iter a na
goj !j !nb =
when (j < lenb) $ do
let !(TU.Iter bj db) = TU.iter b nb
cost = if ai == bj then 0 else 1
x <- (+ 1) <$> VUM.unsafeRead v (v1 + j)
y <- (+ 1) <$> VUM.unsafeRead v (v0 + j + 1)
z <- (+ cost) <$> VUM.unsafeRead v (v0 + j)
VUM.unsafeWrite v (v1 + j + 1) (min x (min y z))
goj (j + 1) (nb + db)
when (i < lena) $ do
VUM.unsafeWrite v v1 (i + 1)
goj 0 0
goi (i + 1) (na + da) v1 v0
gov 0
goi 0 0 0 v_len
VUM.unsafeRead v (lenb + if even lena then 0 else v_len)
where
lena = T.length a
lenb = T.length b
It uses all the familiar tricks and most observations from the jaro
example apply to levenshtein as well. Note that v0 and v1 are merged
into one vector v. So I just add offset equal to length of a single vector
to switch to v1, which is as efficient as swapping pointers.
| Case | Allocated | Max |
|---|---|---|
| levenshtein (C)/5 | 1,208 | 400 |
| levenshtein (C)/10 | 2,256 | 688 |
| levenshtein (C)/20 | 3,904 | 1,096 |
| levenshtein (C)/40 | 5,904 | 1,368 |
| levenshtein (C)/80 | 8,352 | 1,464 |
| levenshtein (C)/160 | 13,232 | 1,656 |
| levenshtein (Haskell)/5 | 2,208 | 400 |
| levenshtein (Haskell)/10 | 4,096 | 688 |
| levenshtein (Haskell)/20 | 7,424 | 1,096 |
| levenshtein (Haskell)/40 | 12,784 | 1,368 |
| levenshtein (Haskell)/80 | 21,952 | 1,464 |
| levenshtein (Haskell)/160 | 40,272 | 1,656 |
Similarly to jaro, Haskell version allocates more but the max residency
stays the same for both C and Haskell implementations.
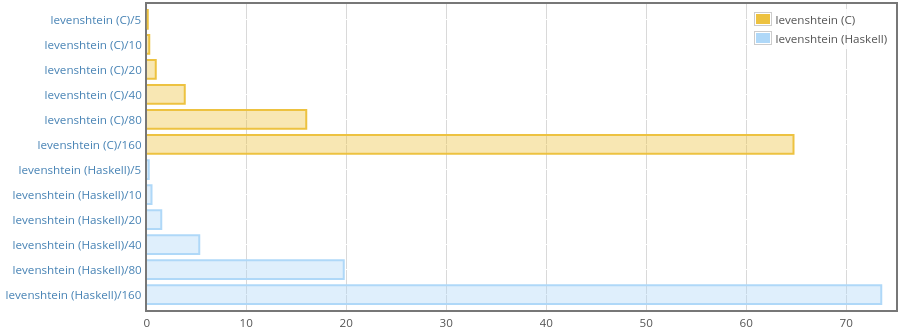
And that’s a win, we are only just a little bit slower than C.
There is also Damerau-Levenshtein distance, but it’s similar (and yet less-readable), so again, let’s skip it in this post.
What’s next?
I compared performance of levenshtein and damerauLevenshtein from
text-metrics with levenshteinDistance defaultEditCosts (marked
“levenshtein (ed)” in the report) from the well-known edit-distance
package:
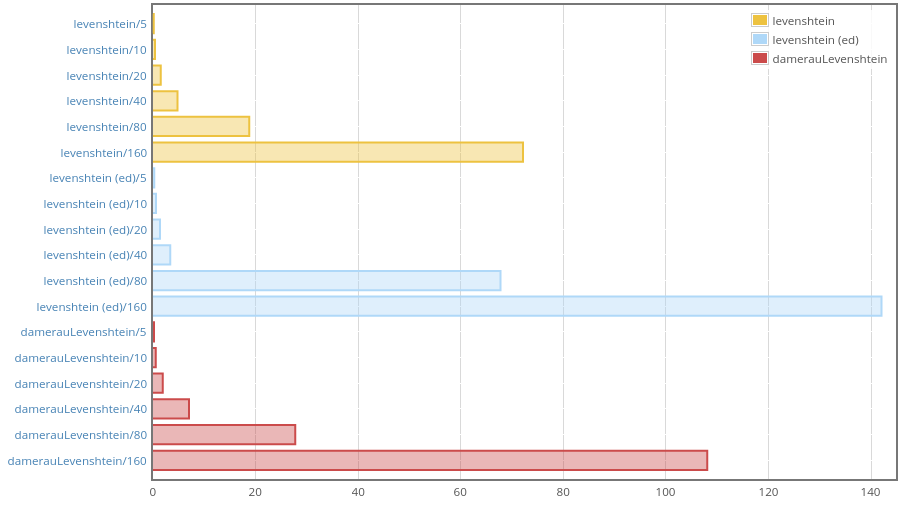
To make the benchmark fair, I fed Text values into text-metrics
functions and Strings into levenshteinDistance. What can we see here?
Clearly, it looks like edit-distance uses two different algorithms. We
beat it in the case of long inputs, with short strings performance is
roughly the same, but for input lengths from 20 to 64 edit-metrics
performs better!
Let’s see the source code:
levenshteinDistance :: EditCosts -> String -> String -> Int
levenshteinDistance costs str1 str2
| isDefaultEditCosts costs
, (str1_len <= 64) == (str2_len <= 64)
= Bits.levenshteinDistanceWithLengths str1_len str2_len str1 str2
| otherwise
= SquareSTUArray.levenshteinDistanceWithLengths costs str1_len str2_len str1 str2
where
str1_len = length str1
str2_len = length str2
It turns out that for the inputs under 64 characters edit-distance uses
the algorithm form this paper. So in the next version of text-metrics
it makes sense to try to use that bit vector algorithm in a similar fashion
and see if it makes things faster.
Conclusion
text-metrics-0.3.0 is written in pure Haskell, almost as fast as the
previous versions (especially for not very long inputs), and is more correct
(we handle characters represented as two Word16 values properly). I have
also added more algorithms which I do not mention here because they were
implemented in Haskell right away. Check the changelog if you’re
interested.